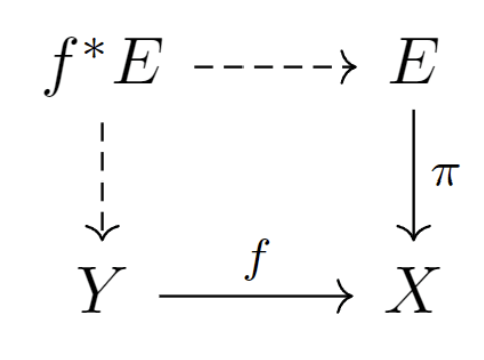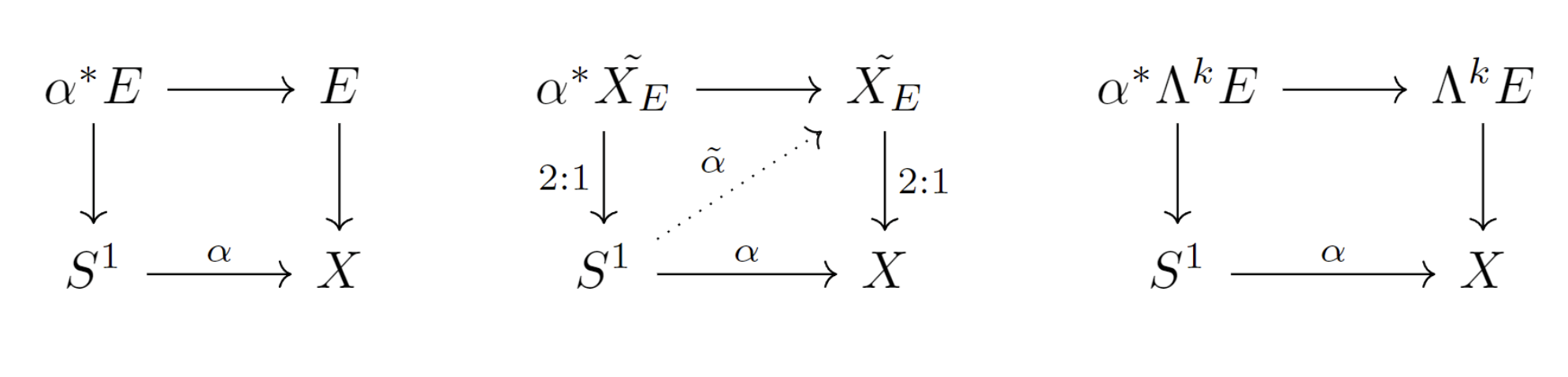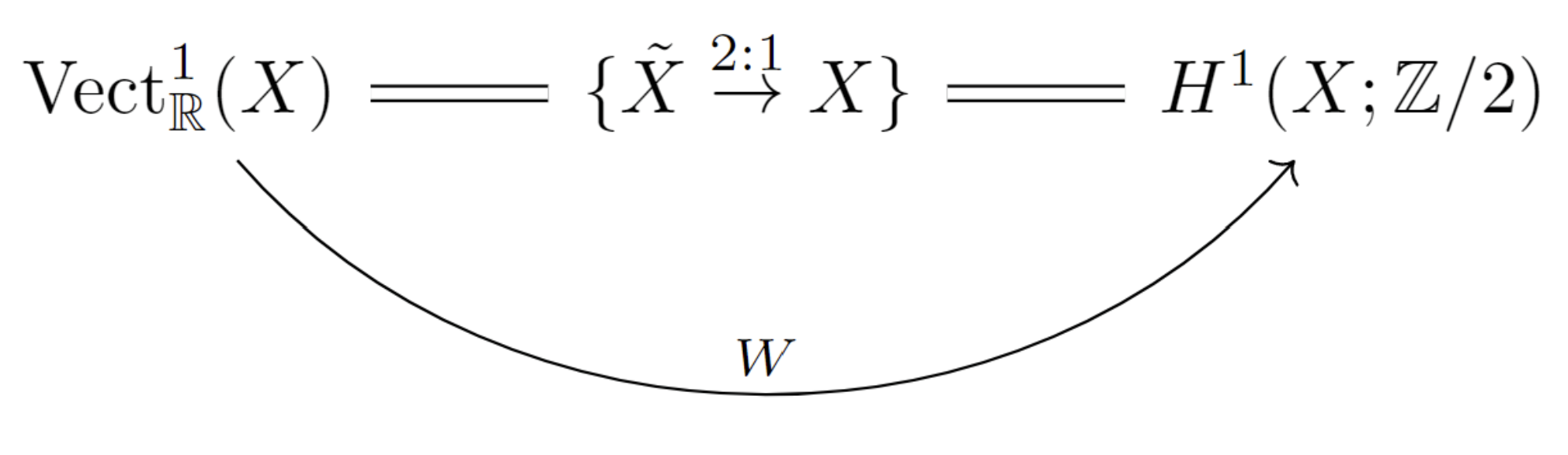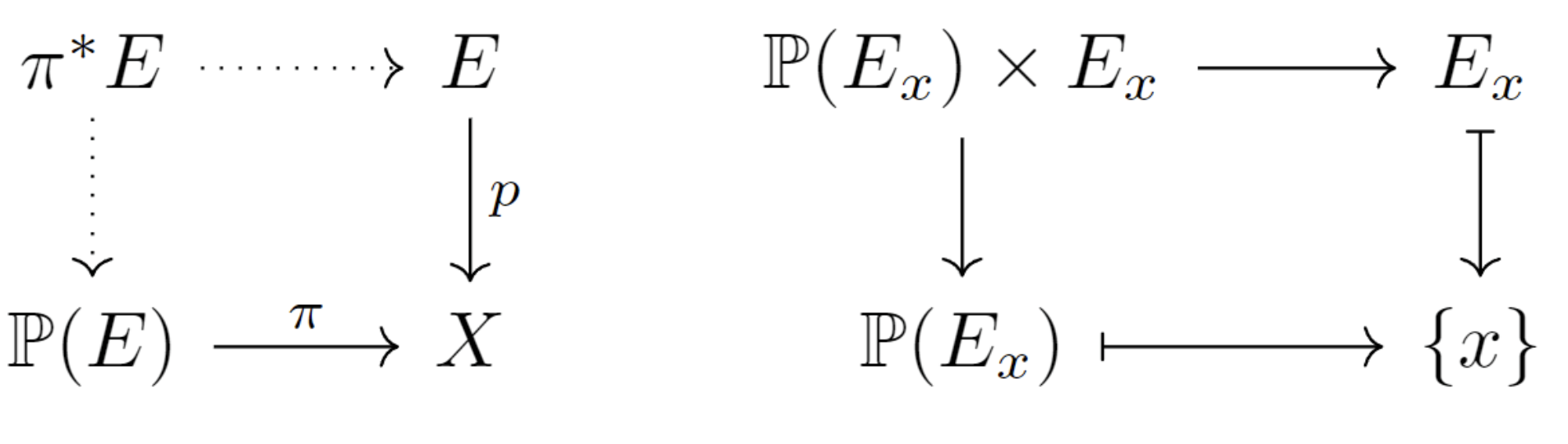Construction of Stiefel-Whitney Classes

Orientation of Vector Bundles

First we shall understand the geometric meaning of Stiefel-Whitney classes on line bundles.

[Def] (Orientable) Let $E\rightarrow X$ be a real vector bundle, with structural group $O(k)$. Say $E$ is orientable if there exists a reduction of structural group to $SO(k)$.

For linear space $V$, define the set of orientation on $V$ to be

$$o(V):=\{(v_1,\cdots,v_k)\text{~is a basis for }V\}/GL_k^+(\mathbb{R})$$

[Def] (Orientation) An orientation of $E$ consists of the following material:

1. $\forall x\in X$, an orientation $\alpha_x\in o(E_x)$;

2. $\alpha$ is locally constant, namely if local trivialization $E_U\cong U\times\mathbb{R}^k$, then $\alpha$ gives

   $$\alpha':U\rightarrow o(\mathbb{R}^k).$$

[Remark] A manifold is orientable if $TM$ admits an orientation. The $k$-th exterior $\Lambda^k E$ of $E$, is also a line bundle over $X$.

[Prop] $E$ is orientable $\Leftrightarrow$ $\Lambda^k E$ is trivial.

Proof. Global section $s:X\rightarrow E$ endows $E_x$ with an orientation. The inverse also holds. $\square$

---

Construction via Orientation

To establish the construction of Stiefel-Whitney class, it requires two important theorem on vector bundles.

[Theorem] (Leray-Hirsch) Let $F\rightarrow P\rightarrow X$ be a fiber bundle, $R$ is a ring. If there exists $u_1,\cdots,u_k\in H^*(P;R)$, such that

$$u_1|_F,\cdots,u_k|_F$$

is a basis for $H^*(F;R)$, then

$$\begin{aligned} H^*(P;R)&\cong H^*(X;R)\otimes R[u_1,\cdots,u_k]\\ \pi^*\alpha\cup u_i&\leftrightarrow \alpha\otimes u_i \end{aligned}$$

Proof. (MV-induction)

1. If $P=X\times F$, then by Kunneth formula, the theorem establishes.
2. Let $X_1,X_2\subset X$​ be subspaces.

Since $M$ is free, then the sequence is exact. $\square$

[Theorem] (Splitting principle) Let $E\rightarrow X$ be a vector bundle of rank $k$ and $f:Y\rightarrow X$.

1. $f^*:H^*(X,\mathbb{Z}/2)\rightarrow H^*(Y,\mathbb{Z}/2)$ is injective;
2. $\exists L_1,\ldots,L_k\rightarrow Y$ are line bundles, s.t.

$$f^*E=L_1\oplus\cdots\oplus L_k.$$

Notice that

$$\begin{aligned} w_1(E)&\in H^1(X,\mathbb{Z}/2)\\ &\cong \mathrm{Hom}(H_1(X,\mathbb{Z}),\mathbb{Z}/2)\\ &=\mathrm{Hom}(\pi_1(X)^{ab},\mathbb{Z}/2)\\ &\cong\mathrm{Hom}(\pi_1(X),\mathbb{Z}/2)\\ &\cong\{2\text{-cover~of~}X\} \end{aligned}$$

Define $\widetilde{X_E}:=\{v\in\Lambda^kE:|v|=1\}\subset\Lambda^kE$ be a 2-cover of $X$. Since element in $\pi_1(X)$ is the map $\alpha:S^1\rightarrow X$.

[Prop] The following statements are equivalent:

1. $\alpha^*E$ is orientable;
2. $\alpha^*\widetilde{X_E}$ is trivial;
3. $\alpha$ can be lifted to $\widetilde{X_E}$.

Thus, $\forall [\alpha]\in\pi_1(X)$, define

$$w_1(E)[\alpha] =\left\{ \begin{aligned} &+1,\qquad \alpha^*E\text{~is orientable},\\ &-1,\qquad \alpha^*E\text{~is unorientable}. \end{aligned} \right.$$

Suppose that $\boxed{E\rightarrow X}$ is a vector bundle of rank $k$, and $L=\boxed{\Lambda^kE\rightarrow X}$. By the above correspondence,

Define

$$w_1(E):=W(\Lambda^kE)$$

which means

$$w_1(E)[\alpha]=\left\{ \begin{aligned} &+1,\qquad \alpha^*E\text{~is orientable},\\ &-1,\qquad \alpha^*E\text{~is unorientable}. \end{aligned} \right.$$

for $\alpha:S^1\rightarrow X$. In fact, $w_1$ gives $\text{Vect}_\mathbb{R}^1(X)\cong H^1(X,\mathbb{Z}/2)$, which means that $w_1$ classifies real line bundles. Now we wish to define all Stiefel-Whitney classes.

[Prop] Let $L_1,L_2\in\text{Vect}_\mathbb{R}^1(X)$. Then

$$w_1(L_1\otimes L_2)=w_1(L_1)+w_1(L_2).$$

Proof. For line bundle, the tensor product of unorientable bundle is orientable. $\square$

Whitney product formula: Notice that $\Lambda^{k+l}(E\oplus F)=\Lambda^kE\otimes\Lambda^lF$. Then

$$\begin{aligned} w_1(E\oplus F) &=w_1(\Lambda^{k+l}(E\oplus F))\\ &=w_1(\Lambda^kE\otimes\Lambda^lF)\\ &=w_1(E)+w_1(F). \end{aligned}$$

Let $E\rightarrow X$ be a real vector bundle of rank $k$. Define

$$\begin{aligned} \mathbb{P}(E)|_x:&=\{\text{lines through the origin of }E_x\}\\ &=\mathbb{P}(E_x) \end{aligned}$$

If $E_U\cong U\times\mathbb{R}^k$, then $\mathbb{P}(E)|_U\cong E\times\mathbb{R}P^{k-1}$ is a vector bundle.

Denote the tautological line bundle over $\mathbb{P}(E)$ by

$$\eta_x:=\{(l,u)\in\mathbb{P}(E_x)\times E_x|u\in L\}$$

Define

$$\begin{aligned} L_E:&=\{(l,u)\in\mathbb{P}(E)\times E|\pi(l)=p(u), u\in l\}\\ &\subset \pi^*E \end{aligned}$$

Then $\boxed{L\rightarrow\mathbb{P}(E)}$ is a line bundle. Consider the tautological line bundle over $\mathbb{R}P^n$:

$$\eta_n\rightarrow \mathbb{R}P^n$$

Non-zero: since $\eta_1\rightarrow\mathbb{R}P^1$ is a Mobius line bundle, which is unorientable, then $w(\eta_1)=a\neq 0$. With the natural embedding $i:\mathbb{R}P^1\rightarrow \mathbb{R}P^n$, we have

$$w_1(\eta_n)=a\neq 0\in H^1(\mathbb{R}P^n,\mathbb{Z}/2).$$

Pullback: Let $f:X\rightarrow Y$ and $\alpha:S^1\rightarrow X$ be a loop.

By direct calculation:

$$w_1(f^*E)[\alpha]=\left\{ \begin{aligned} &+1, \qquad (\alpha^*f^*)E\text{~is~orientable};\\ &-1, \qquad (\alpha^*f^*)E\text{~is~unorientable}. \end{aligned} \right.$$

$$(f^*w_1(E))[\alpha]=\left\{ \begin{aligned} &+1, \qquad (f\circ\alpha)^*E\text{~is~orientable};\\ &-1, \qquad (f\circ\alpha)^*E\text{~is~unorientable}. \end{aligned} \right.$$

Hence $w_1(f^*E)=f^*w_1(E)$. Then $\{1,w_1(\eta_n),\cdots,w_1(\eta_n)^{n-1}\}$ is a basis for $H^*(\mathbb{R}P^n;\mathbb{Z}/2)$, and

$$\{1,w_1(L_E),\cdots,w_1(L_E)^{k-1}\}$$

is a basis for $H^*(\mathbb{P}(E_x);\mathbb{Z}/2)=H^*(\mathbb{R}P^{k};\mathbb{Z}/2)$. By Leray-Hirsch Theorem,

$$\begin{aligned} H^*(\mathbb{P}(E);\mathbb{Z}/2) &\cong H^*(X)\otimes \mathbb{Z}/2\{1,w_1(L),\ldots,w_1(L)^{k-1}\}\\ \pi^*\alpha\cup w_1(L)^s&\leftarrow \alpha\otimes w_1(L)^s \end{aligned}$$

where $\pi^*:H^*(X;\mathbb{Z}/2)\rightarrow H^*(\mathbb{P}(E);\mathbb{Z}/2)$ is injective.

The injectivity is by $\pi^*(H^*(X;\mathbb{Z}/2))=H^*(X)\otimes\mathbb{Z}/2$​.

Thus,

$$w_1(L_E)^k=(\pi^*a_1)w_1(L_E)^{k-1}+\cdots+(\pi^*a_{k-1})w_1(L_E)+\pi^*a_k.$$

Define the $i$-th Stiefel-Whitney class by

$$w_i(E):=a_i,\qquad 1\leq i\leq k.$$

---

Respecting Axioms

We are now in a position to show that: the Stiefel-Whitney classes defined above satisfies Axioms. In the previous part, we have verified the nontrivality, pullback of $w_1$ and Whitney product formula for line bundle.