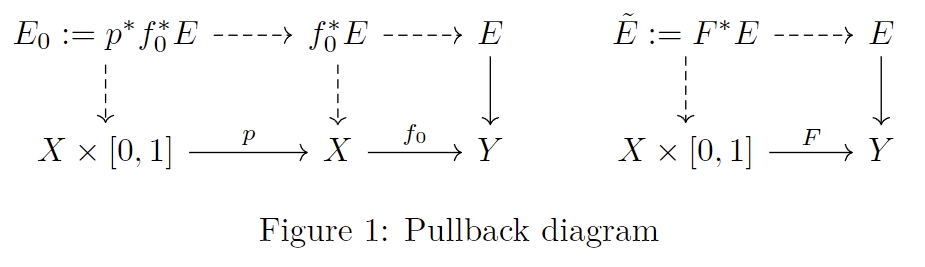Introduction to Vector Bundle

Stiefel-Whitney classes are defined on vector bundle. First we consider some properties of vector bundle. There is no gap between Vector Bundle ABC and Vector Bundle DEF, as they are designed for you to take a break.

---

Vector Bundle ABC

Fix a topological space $B$, called base space.

[Def] (Real vector bundle) A real vector bundle $\xi$ over $B$ consists of the following data:

1. Total space: $E(\xi)$, a topological space;
2. Projection map: $\pi:E\rightarrow B$ a continuous map;
3. $\forall b\in B$, the $\mathbb{R}$-vector space structure on $\pi^{-1}(b)$,

such that: $\forall p\in B$, $\exists U\subset B$ an open neighborhood of $p$ and an integer $k\geq 0$, and a continuous map

$$h:U\times \mathbb{R}^n\rightarrow \pi^{-1}(U)$$

such that $\boxed{h(b.\cdot):\mathbb{R}^n\rightarrow\pi^{-1}(b)}$ defines an $\mathbb{R}$-isomorphism of vector spaces for each $b\in U$. Here $\pi^{-1}(b)$ is called the fiber over $b$, denoted by $F_b$ or $F_b(\xi)$. Clearly, $F_b\neq\emptyset$.

[Remark] $\dim(F_b)$ is a locally constant function of $b$​.

[Remark] $\mathbb{R}^n$-bundle is the special case for fiber bundle, with fiber $\mathbb{R}^n$ and structural group $\mathrm{GL}(n,\mathbb{R})$.

[Def] (Isomorphic vector bundle) If there exists $f:E(\xi)\rightarrow E(\eta)$, a homomorphism between total spaces, that restricted to isomorphisms

$$f|_{F_b(\xi)}:F_b(\xi)\rightarrow F_{f(b)}(\eta)$$

on each fiber over each point $b\in B$, then $\xi$ is isomorphic to $\eta$, denoted $\xi\simeq\eta$.

[e.g.] (Trivial bundle) Define the trivial bundle over $B$ by setting total space $E=B\times\mathbb{R}^n$ and projection map

$$\begin{aligned} \pi:E&\rightarrow B\\ (b,v)&\mapsto b \end{aligned}$$

[e.g.] (Tangent bundle) $E=TM$​ and

$$\begin{aligned} \pi:TM&\rightarrow M\\ (x,v)&\mapsto x \end{aligned}$$

The fiber over $x$ is $\pi^{-1}(x)=\{(x,v):v\in T_xM\}$ with a canonical structure. The local triviality can also be verified. Such bundle is denoted by $\tau_M$.

[Def] (Parametrizable) If a smooth manifold $M$ has a trivial tangent bundle $\tau_M$, then $M$ is said to be parametrizable.

[e.g.] (2-dimensional unit ball) $S^2\subset\mathbb{R}^3$ is not parametrizable. In general, parametrizable manifolds must have Euler characteristic $0$, namely, $\chi(S)=0$. However, $\chi(S^2)=2$.

[e.g.] (Normal bundle) Let $M\subset\mathbb{R}^n$ be a smooth submanifold. The normal bundle of $M$, denoted $\nu_M$, is defined as follows:

1. $E=\{(x,v):v\in\mathbb{R}^n,v\perp T_xM\}$;
2. $\pi(x,v)=x$

It can be verified that $\pi^{-1}(x)$ has a $\mathbb{R}$-vector space structure. It suffices to verify local triviality.

[e.g.] (Canonical line bundle over $\mathbb{P}^n$) Define base space

$$\mathbb{P}^n:=\{x\in S^n\subset\mathbb{R}^{n+1}\}/\{x,-x\}$$

with total space

$$E(\gamma_n^1)=\left\{\left(\{\pm x\},v\right)\in\mathbb{P}^n\times\mathbb{R}^{n+1}:v=\lambda x, \lambda\neq 0\right\}$$

and projection map

$$\begin{aligned} \pi:E&\rightarrow B\\ (\{\pm x,v\})&\mapsto \{\pm x\} \end{aligned}$$

Here $\pi^{-1}(x)$ can be viewed as “line through $x$ and $-x$ in $\mathbb{R}^{n+1}$”, and thus with a natural $\mathbb{R}^1$-structure. Such line bundle is called the canonical line bundle over $\mathbb{P}^n$, denoted $\gamma_n^1$.

[Theorem 1] $\gamma_n^1$ is not a trivial bundle over $\mathbb{P}^n$, for $n\geq 1$.

The proof of the above theorem requires the notion of cross section, a generalization of vector field, to describe the condition of trivial bundle.

[Def] (Cross section) A cross section of a vector field $\xi$ with base space $B$ is a map

$$s:B\rightarrow E(\xi)$$

such that

$$s(b)\in F_b(\xi), \quad \forall b\in B$$

Proof of Theorem 1. Notice that there exists a nowhere zero cross section over trivial $\mathbb{R}$-bundle. It suffices to show that: there does not exist “nowhere zero cross section”. Let $s:\mathbb{P}^n\rightarrow E(\gamma_n^1)$ be a cross section. Then

$$\begin{aligned} S^n\rightarrow&\mathbb{P}^n\overset{s}{\rightarrow}E(\gamma_n^1)\\ x\mapsto&\{\pm x\}\mapsto (\{\pm x\},\tilde{s}(x)) \end{aligned}$$

where $\tilde{s}(x)\neq 0$ has the same direction of $x$, i.e. $\exists t:S^n\rightarrow\mathbb{R}-\{0\}$, s.t.

$$\tilde{s}(x)=t(x)x$$

with the property that $t(-x)=-t(x)$. Since $t\in C^0$, then by intermediate value theorem, $\exists x_0\in S^n$, s.t. $t(x_0)=0$. Contradiction! $\square$​

[Prop] Let $E$ be a vector bundle over $B$ with rank $k$, $U\subset B$ be a open subset of $B$. Then $E_U\cong U\times\mathbb{R}^k$ iff $\exists s_1,\ldots,s_k\in\Gamma(E_U)$, s.t. $\forall x\in U$, $\{s_1(x),\ldots,s_k(x)\}$ are linearly independent.

---

Vector Bundle DEF

[Def] (Quotient bundle) Let $F\hookrightarrow E$, define the fiber over $x\in B$ to be $(E/F)_x:=E_x/F_x$, total space $E/F=\bigsqcup E_x/F_x$, and $\pi$ as usual.

Suppose that $E$ and $F$ have rank $k$ and $l$ , respectively. The linear space structure on $(E/F)_x$ is given by the canonical quotient on linear spaces. We shall use the proposition to verify the local triviality of $E/F$. $\forall x\in X$, $U\subset B$ be a open neighborhood of $x$.

---

More on Cross Section

Before we continue to further topics, we shall look into further theorems and propositions on cross section.

[Prop] Let $E\rightarrow X$ be a vector bundle, where $X$ is compact and Hausdorff. Let $Y\subset X$ be a closed subset of $X$, and $E|_Y$ be the restriction vector bundle. Suppose that $s\in\Gamma(E|_Y)$. Then $\exists\bar{s}\in\Gamma(E)$, s.t.

$$\bar{s}|_Y=s.$$

[Remark] In fact, we can only require $X$ to be paracompact. In a $T^4$ topological space, according to Tietz Theorem, any function can be extended to a global function.

[Remark] For other cases, when a space is compact + Hausdorff, we can think of method of partition of unity: first prove the theorem locally, and glue the local cases together with partition of unity.

Proof of Prop.

---

Homotopy Invariance

In this part, we shall prove that “pullback has homotopy invariant”.

[Theorem 2] (Homotopy Invariance)

Let $X$ be a compact and Hausdorff space, $f_0,f_1:X\rightarrow Y$, and $F:f_0\simeq f_1$. Namely,

$$\begin{gathered} F:X\times[0,1]\rightarrow Y\\ F|_{X\times\{0\}}=f_0,\quad F|_{X\times\{1\}}=f_1 \end{gathered}$$

Let $E\rightarrow Y$ be a vector bundle over $Y$. Then $f_0^*E\cong f_1^*E$.

Proof. Define $\iota_t:X\rightarrow X\times [0,1]$ by $\iota_t(x)=(x,t)$. Then

$$\begin{gathered} \iota_0^*(F^*E)=f_0^*E\\ \iota_1^*(F^*E)=f_1^*E\\ \end{gathered}$$

We shall prove that $\tilde{E}:=F^*E$ has the “same” section on every restriction $\tilde{E}|_{X\times\{t\}}$. Define $E_0:=p^*f_0^*E$ be another vector bundle over $X\times [0,1]$.

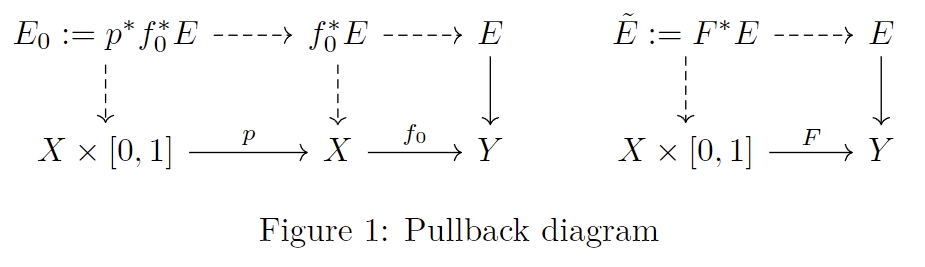
Goal: Prove that $\tilde{E}|_{X\times\{t\}}\cong E_0|_{X\times\{t\}}$ . Consider the $\mathrm{Hom}$-bundle

$$\mathrm{Hom}(E',E_0)\rightarrow X.$$

If $t\in[0,1]$ satisfies that $\tilde{E}|_{X\times\{t\}}\cong E_0|_{X\times\{t\}}$, then by the correspondence, $\exists s\in\Gamma(\mathrm{Hom}{(E',E_0)}|_{X\times\{t\}})$, such that $s$ is an isomorphism on each fiber over $X\times\{t\}$. By Prop in cross section, since $X\times\{t\}$ is a compact set in $X$, then $s$ can be extended to a cross section $\bar{s}\in\Gamma(\mathrm{Hom}(\tilde{E},E_0))$.

Consider

$$W:=\left\{(x,t)\in X\times[0,1]:\bar{s}|_{\mathrm{Hom}(\tilde{E},E_0)_{(x,t)}}\text{~isomorphic}\right\}$$

Openness: since $\bar{s}$ is a cross section, then $\bar{s}$ depends on $(x,t)$ continuously, which implies that $\det(\bar{s})\neq 0$ is an open condition. Thus $W$ is an open set.

Since $X\times\{t\}\subset W$ is compact, then by Tubular Neighborhood Theorem, $\exists \varepsilon>0$, s.t.

$$X\times (t-\varepsilon,t+\varepsilon)\subset W.$$

Therefore, using isomorphism $\bar{s}$, we know that

$$J:=\{t\in[0,1]:\tilde{E}|_{X\times\{t\}}\cong E_0|_{X\times\{0\}}\}\subset [0,1]$$

is open and closed, which means that the restriction map is locally constant into $\mathrm{Vect}_\mathbb{R}(X)$. Thus $J=[0,1]$, and we prove that $\tilde{E}|_{X\times\{t\}}$ does not depend on $t$, which implies that

$$f_0^*E=E'|_{X\times\{0\}}\cong E'|_{X\times\{1\}}=f_1^*E.$$

This completes the proof. $\square$