本文中所称「流形」均为带边拓扑流形。
一种最常用的得到新三维流形的办法是:取出两个定向带边三维流形$M_1$和$M_2$,具有同胚的边界$\partial M_1\approx\partial M_2=\Sigma_g$,将这两个流形沿着边界,用某个同胚$f:\Sigma_g\rightarrow \Sigma_g$粘接起来,得到闭三维流形
$$
M:=M_1\cup_f M_2.
$$
并且领结引理告诉我们:粘接映射的同痕类$[f]\in\mathrm{Mod}(\Sigma_g)$决定了产出流形$M$的同胚型。回过头来问:什么样的三维流形$M_1$以$\Sigma_g$为边界?自然会想到实心环面及其边界和,这就把所有信息确定了:如果一个三维流形$M$可以通过两个相同的实心环面,由$f\in\mathrm{Mod}(\Sigma_g)$粘接边界得到,那么这样的拆分方法就称为这个三维流形$M$的Heegaard分解。
然而,定义并不保证所有的三维流形都能够这样拆分,欲行Heegaard分解事,还需下面的定理。
Theorem. 任意三维流形都有Heegaard分解。
Proof. 有结果说「任意三维流形都有三角剖分」,我们基于该结果给出一个构造性证明。取定三维流形$M$的一个三角剖分T,将T的所有信息进行如下改造:
- 顶点:替换为$D^3$;
- 边:替换为$D^2\times I$,想象一个长而细的圆柱,两头凹陷;
- 三角形:替换为$\Delta\times I$,想象一个咬了三口的发糕;
- 三棱锥:替换为$D^3$。
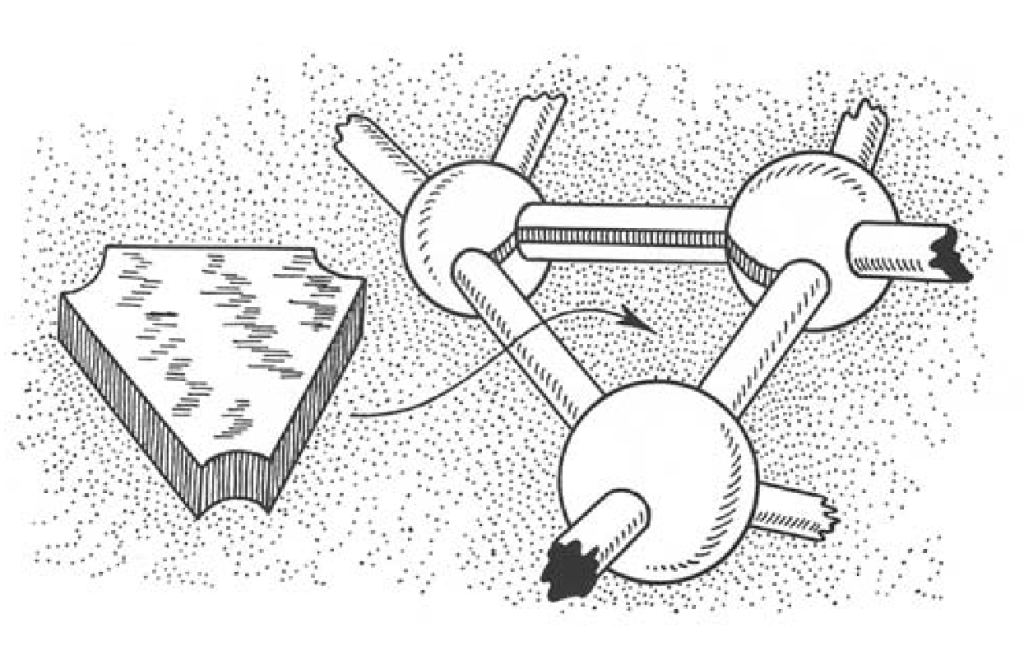
如此,可令$H(T)$为所有顶点和边的替换构成的2-handlebody,$H'(T)$为三角形和三棱锥替换构成的handlebody。这样一来,三角剖分给出了边界粘接的方法,如此得到Heegaard分解。$\square$
一个流形上可能存在很多不同的Heegaard分解。比如,给定一个Heegaard分解$M=H_g\cup_f H_g$,考虑$\mathrm{Mod}(\Sigma_g)\rightarrow\mathrm{Mod}(\Sigma_{g+1})$自然嵌入,于是可以通过平凡粘接环面 (add unknotted 1-handle),来使得Heegaard分解的亏格增长
$$
M=H_{g+1}\cup_{f’} H_{g+1}
$$
这样的过程称为稳定化。如果两个Heegaard分解能通过稳定化得到同一个Heegaard分解,那么这两个Heegaard分解称作是稳定等价的。事实上:
Theorem. 同胚的三维流形的不同Heegaard分解之间是稳定等价的。
Proof. 证明分为两步
- 由三角剖分$T$和$T’$得来的Heegaard分解是稳定等价的;
- 对于任意Heegaard分解,存在某个三角剖分$T$,使得该Heegaard分解与$T$给出的Heegaard分解时稳定等价的。
第一步的证明依靠「任意两个三角剖分可以通过重心剖分 (barycentric subdivision),找到共同的子三角剖分」,并且重心剖分可以用「粘接unknotted 1-handle」实现。
第二步的证明:先取定
- Heegaard分解$M=H_g\cup H’_g$;
- $\Gamma$:1-柄体$H_g$的一个「轴心图」,那么$\Gamma$就是一个只有一个顶点和$g$条闭曲线的图;
- $T$:$M$的三角剖分,使得$H_g$和$H_g’$都是子复形;
令$\tau=T|_{H_g}$和$\tau’=T|_{H’_g}$,那么通过适当取子剖分,可以使得$\tau$满足下面条件(a),$\tau’$满足下面条件(b)。
(a) $\tau^{(1)}$的三维加厚,可以由$\Gamma$的三维加厚,仅通过粘接unknotted handles得到;
(b) $\tau’^{(1)}$的三维加厚,可以由$\tau’^{(1)}|_{\partial H’_g}$的三维加厚,仅通过粘接unknotted handles得到;
记「加厚」为$U(\cdot)$,因为$\tau’$满足条件(b),并且$\tau’$与$\tau$在边界上相等,所以
$$
\begin{aligned}
U(\tau’^{(1)})&=U(\tau’^{(1)}|_{\partial H_g})\cup\text{unknotted 1-handles}\\&=U(\tau^{(1)}|_{\partial H_g})\cup\text{unknotted 1-handles}\\
\end{aligned}
$$
另外,$\tau$又满足条件(a),且$\tau$和$\tau’$合起来得到整个$T$,所以
$$
\begin{aligned}
H(T)=U(T^{(1)})&=U(\tau^{(1)})\cup\text{{unknotted 1-handles}}\\
&=U(\Gamma)\cup\text{更多unknotted 1-handles}\\
&=H\cup\text{更多unknotted 1-handles}
\end{aligned}
$$
即是说给定的Heegaard分解,和$T$给出的Heegaard分解稳定等价,这就完成了证明。$\square$