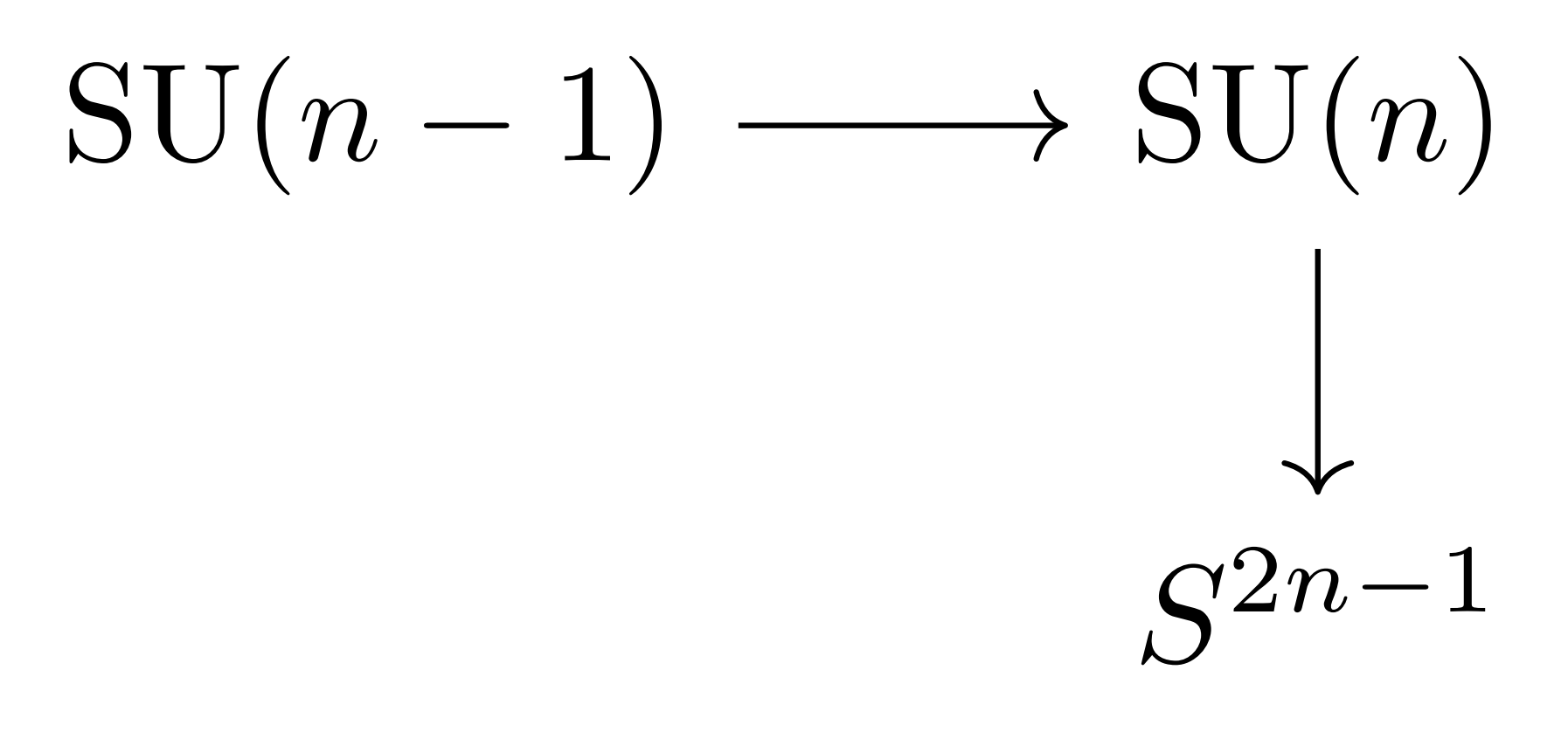Spectral sequences: computation of cohomology ring

To be completed.

Being a fancy technique in computing cohomology ring $H^*$ in algebraic topology, spectral sequences are more generalized and thus more abstract than, somehow its prototype, long exact sequences. This post is to demonstrate some useful results in algebraic topology that can be computed with spectral sequences.

---

What is spectral sequence?

Let $R$ be a commutative ring with identity. A homological spectral sequence contains the following information:

1. A family of $R$-modules $E_{*,*}^r$ with differential

$$d^r:E^r_{p,q}\rightarrow E_{p+r,q+r-1}^r$$

where $r$ is a positive integer called page. We say $\{E^r_{*,*},d^r\}$ is a homological spectral sequence.

2. The relation between $r$-th page and $(r+1)$-th page is as follows

$$E_{p,q}^{r+1}:=H(E_{p,q}^{r+1},d^r)$$

More precisely, the $(p,q)$-term on the $(r+1)$-th page is the homology of the $r$-th page:

$$E_{p,q}^{r+1}=\frac{\ker(d^r:E_{p,q}^r\rightarrow E^r_{p+r,q-r+1})}{\mathrm{im}(d^r:E^r_{p-r,q+r-1}\rightarrow E^r_{p,q})}.$$

Similarly, we can define a cohomological spectral sequence $\{E_r^{*,*},d_r\}$​​​. Note that compared with homology, cohomology has a natural ring structure, which leads us to the world of algebras and multiplication.

Cohomological spectral sequences are mainly used in the future.

Assumption. To put the above definition in use, we have to restrict to relatively “good” spectral sequences. Thus the following assumptions are required for the discussion.

1. (First quadrant) For $p<0$ or $q<0$, assume that $E_{p,q}^r=0$ for every $r$​​.
2. (Stable) For sufficiently large $r$​, all but finitely many differentials on each column are nontrivial.

For fixed non-negative integers $p$ and $q$, there exists $R>0$, such that $\forall r>R$,

$$d^r_{p,q}:E^r_{p,q}\rightarrow E^r_{p+r,q-r+1}$$

and

$$d^r_{p+r,q-r+1}:E^r_{p+r,q-r+1}\rightarrow E^r_{p,q}$$

are trivial maps. Therefore,

$$E^{r+1}_{p,q}=H(E^r_{p,q},d^r)=\frac{\ker(d^r_{p,q})}{\mathrm{im}(d^r_{p+r,q-r+1})}=E_{p,q}^{r+1}.$$

Actually, we have the above equation for each $r>R$, which means that for each $p,q$, the $R$-module stabilizes eventually. Therefore, we can define the infinity page $E_{p,q}^\infty$ as

$$E_{p,q}^r=E^{r+1}_{p,q}=\cdots=:E_{p,q}^\infty.$$

---

Convergent spectral sequences are of the main focus. Take cohomological spectral sequences for instance.

Def. (Convergence). Let $\{E_r^{*,*},d_r\}$ be a cohomological spectral sequence and $H^*$ be a filtered $R$-module with filtration

$$H=F^0H\supset F^1H\supset\cdots\supset F^m H\supset F^{m+1}H=\{0\}$$

Say $\{E_r^{*,*},d_r\}$ converges to $H^*$ if the infinity page of $E$ satisfies

$$E_\infty^{p,q}\simeq F^pH^{p+q}/F^{p+1}H^{p+q}.$$

---

Preparation

We introduce some theorem, perhaps without proofs.

Theorem. Let $F\rightarrow E\rightarrow B$ be a fibration. If $\pi_1(B)$ acts on $H^*(F)$ trivially (lacking definition here), then there exists a cohomological spectral sequences $\{E_r^{*,*},d_r\}$ with

$$E_2^{p,q}=H^p(B;H^q(F;\mathbb{Z}))$$

such that $E_r^{*,*}$converges to $H^*(E;\mathbb{Z})$​​, as a graded-commutative graded algebras.

Lemma. Let $\{E_r^{p,q},d_r\}$ be a first quadrant cohomological spectral sequence converging to a graded algebra $H^*$. If the infinity page $E_\infty^{*,*}$ is a free graded-commutative bigraded algebra, then

$$H^*\cong \mathrm{Tot}(E_\infty^{*,*})$$

as a free graded-commutative graded algebra.

---

Cohomological ring of $\mathrm{SU}(n)$

In this section, we shall compute the cohomology ring $H^*(SU(n),R)$, where $R$ is a commutative ring. Denote $\Lambda(y_{2k+1})$ be the exterior $R$-algebra generated by an element $y_{2k+1}$, where the degree of $y_{2k+1}$ is $|y_{2k+1}|=2k+1$. We shall prove by induction that

$$H^*(\mathrm{SU}(n);R)\cong\Lambda(x_3,\ldots,x_{2n-1})$$

1. $n=2$, $SU(2)\cong S^3$. By knowledge in algebraic topology, $H^*(SU(2);R)\cong \Lambda(x_3)$.
2. Consider the fibration

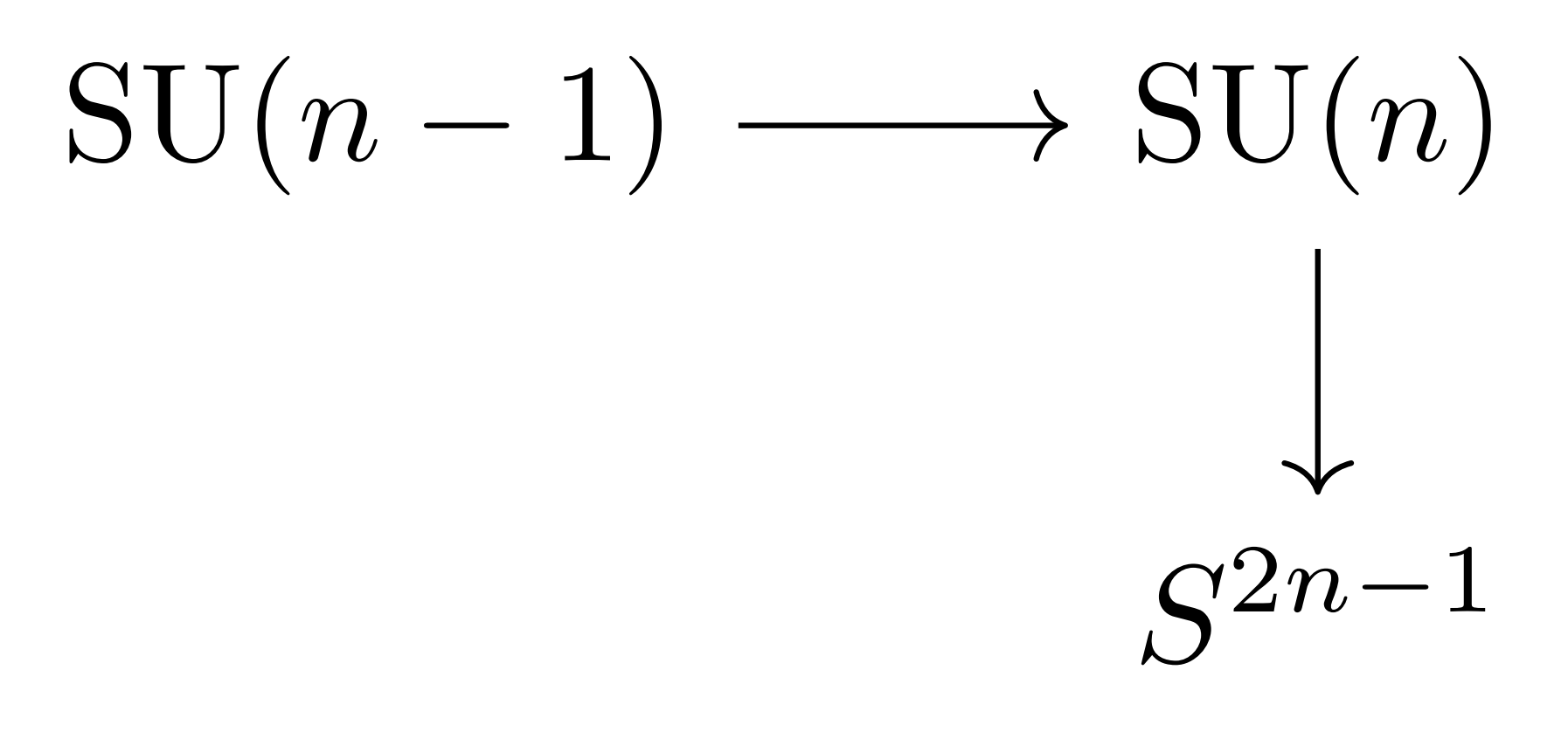
Since for $n\geq 2$, $S^{2n-1}$ is simply-connected, then apply the theorem: there exists a first quadrant cohomological spectral sequence with second page

$$E_{2}^{*,*}=H^*(B;H^*(F;R))=H^*(S^{2n-1};H^*(SU(n-1);R)).$$

Using universal coefficient theorem, with $H^*(SU(n-1);R)$ is free,

$$0\rightarrow H^n(X)\otimes G\rightarrow H^n(X;G)\rightarrow \mathrm{Tor}(H^{n+1}(X),G)\rightarrow 0$$

then

$$E_{2}^{*,*}=H^*(S^{2n-1};H^*(SU(n-1);R))=H^*(S^{2n-1})\otimes H^*(SU(n-1);R).$$

By induction,

$$E^{*,*}_2\cong\Lambda(y_{2n-1})\otimes\Lambda(x_3,x_5,\ldots,x_{2n-3})$$

Claim. All differentials are zero.

Proof of Claim. All differentials $d_r$ are zero, except for $r=2n-1$, as only the $0$-th column and the $(2n-1)$-th column are non-zero. Write the generating element in the first column as $x_{2k-1}\in E_2^{0,2k-1}$, for $k=1,2,\cdots,n-1$. Then

$$d_{2n-1}x_{2k-1}\in E_2^{2n-1,2k-2n}=0$$

Therefore, by Leibnitz’s rule, we obtain $d_{2n-1}=0$ as well. Thus all differentials are zero. $\square$

With the claim, we have

$$E_\infty^{p,q}=E_2^{p,q}=E^{*,*}_2\cong\Lambda(y_{2n-1})\otimes\Lambda(x_3,x_5,\ldots,x_{2n-3})$$

By lemma, we have

$$H^*(SU(n);R)\cong\mathrm{Tot(\Lambda(y_{2n-1})\otimes\Lambda(x_3,x_5,\ldots,x_{2n-3}))}\cong\Lambda(x_3,x_5,\ldots,x_{2n-1}).$$

This completes the proof.

---

Cohomology ring of $BU(n)$